学会発表をする際には、相関係数を求めることが多いですが、いざ相関係数を求めるときに、
ピアソン?スピアマン?
どちらの相関係数を求めればいいの?と思ったことはないでしょうか
ここでは、EZRで算出できる(検定できる)相関係数の種類を説明するとともに、どの相関係数を使用すべきか解説しています。
相関とは
相関は2つの変数の関係性を評価するものであり、2つの変数間の因果関係を示すのではありません。
相関係数で関連性の強さを評価します。
例えば、
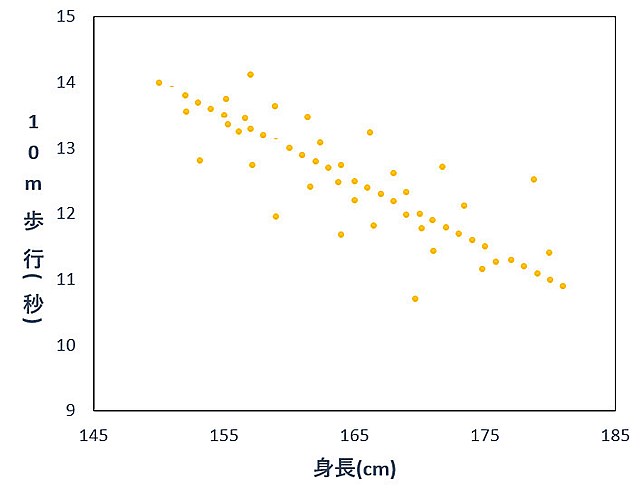
ある地域に在住している人に対して、身長と10m歩行のデータを収集した場合(下図)、
身長と10m歩行に負の相関関係があれば、身長が高いほど10m歩行が速いとは言えます。
しかし、下記のグラフを見て、身長155cmの人は、10m歩行が13.4秒と予測することはできません。
これをするには、「回帰分析」をする必要があります。
相関係数とは
相関係数とは相関の強さを表す係数です。
相関係数にはいくつかありますが、一般的にピアソンの積率相関係数をさしています。
相関係数は-1から1の値の間をとります。
また、相関係数は外れ値の影響を受けるので、外れ値の検定をする必要性があります(場合によってはしなくてもよい)。
相関係数の種類
リハビリテーションでよく使用されている相関係数は、Pearson(ピアソン)の積率相関係数, Spearman(スピアマン)の順位相関係数です。
EZRではこれらの相関係数の値を求め、検定をすることができます。
Pearson(ピアソン)の積率相関係数
ピアソンの積率相関係数を求めるには、変数が連続変数である必要性があります。
また、変数は正規分布に従っている必要があります。
*連続変数とは、量的なデータのことです。
数値で表す事ができます。主に間隔尺度や比率尺度をさしています(厳密には少し違うと思います)。
名義尺度や順序尺度は質的データなので、連続変数ではないので、ピアソンの積率相関係数は使用できません。

順位相関係数(SpearmanとKendallの順位相関係数)
順位相関係数は、スピアマンとKendall(ケンドール)の順位相関係数が代表例で、EZRでも使用できます。
特徴としては、変数が連続変数でない場合や変数が正規分布をしていなくても使用できます。
そして、変数に順位がついていれば使用できます。
FIMは1点、2点と順位はついていますが、点数と点数の間隔には意味がないので連続変数ではありません。
このため、スピアマンの積率相関係数は使用せずに、順位相関係数を使用する必要があります。
尺度の話はこちらで解説しています↓

EZRでの相関係数の算出と検定方法
EZRでは、相関係数の算出と検定を同時に行うことができます。
Pearson(ピアソン)の積率相関係数の場合
詳細は別ページに記載予定です。
順位相関係数(SpearmanとKendallの順位相関係数)の場合
詳細は別ページに記載予定です。
参照・参考文献・書籍
今回の記事は、下記の文献や書籍を参照・参考にしています。
・EZRでやさしく学ぶ統計学~EBMの実践から臨床研究まで~, 神田善伸,2014 p211
・すぐできる!リハビリテーション統計,山本澄子,2013
・光永貴之: 使える統計学基本講座(第2回)-相関と直線回帰-. 農作業研究45(1): p53-62, 2010
・戸田準: データ解析入門3.日本家政学会誌 51(6): p539-544, 2000
〇EZRを漫画で勉強できる本
〇初級から中級者用の解説書
〇中級から上級者用の解説書(私はこれで勉強しました)